前回から、「児童期前半の重要な学習」として欠かせない要素をピックアップし、それぞれどのような取り組みが望ましいか、そしてそれはなぜかということをお伝えしています。第1回目（前回）は、学問の手段となる読み書きの基盤を築くことの重要性についてお伝えしました。今回は、「確かな計算力を身につける」をテーマに掲げ、望ましい計算力とはどのようなものか、そしてそれが先々の算数・数学学習にどのような影響を及ぼすかについてともに考えていただこうと思います。

まずは余談から。算数の醍醐味について考えさせられた小さなできごとがあります。それは、私が中学受験専門の進学塾に勤務していたときのことです。あるおかあさんから、「テキストの課題の解答・解説を予め１年分譲ってほしい」と依頼されました（当時、テキストの問題の解答と解説は、毎回の授業ごとに配布していました）。その理由として、こんなことをおっしゃいました。

「毎週配られる算数の解答・解説を見るたびに、『こんな着眼のしかたや解法があるのか！？』と、感心してしまいます。『ああ、子どもの頃にこんな指導を受けていたなら、私は算数・数学が得意な人間になり、全然違う人生を歩んでいただろうに…』と思うと残念でたまりません。いっそ、テキストの解答と解説を１年分まとめて私にくださいませんか？ 私が家で息子に教えてやりたいんです！」

算数の魅力は、着眼や解法を発見したときの喜びや感動にあります。それを味わう経験の積み重ねが算数学力を飛躍的に伸ばすのです。おかあさんが教えてしまうと、息子さんは算数学力を飛躍させるうえで必須の体験ができません。そう考え、私は丁重にお断りしました（おかあさんの熱心さには頭の下がる思いをしましたが）。

本題に入ります。言うまでもありませんが、掛算九九や筆算は算数の基礎学力形成に欠かせないもので、低学年児童期の算数学習の要に位置づけられています。これらは反復練習の継続で習熟していく必要があります。そのためでしょうか。機械的に覚え込むことに明け暮れたり、延々と同じような作業をくり返したりするような取り組みを大人が課しているケースがかなりあるようです。こうした勉強だけではほんとうの計算力は身につきません。では、確かな計算力とはどのようなものでしょうか。

九九を例にあげてみましょう。「いんいちがいち」、「いんにがに」、と順を追って進み、「くくはちじゅういち」まで連続して空で言えるようになったら「九九は卒業」でしょうか。実際のところ、これだけでは十分とは言えません。「くくはちじゅういち」、「くはしちじゅうに」、「くしちろくじゅうさん」…と逆向きに下がりながら、「いんいちがいち」までよどみなく言えるようになる必要があります。さらに、「ろくろくさんじゅうろく」「しろくにじゅうし」「ごはよんじゅう」など、ランダムにも自在に言えなければ実際の役には立ちません。これらが臨機応変にできて初めて「九九をマスターした」と言えます。九九は様々なシチュエーションで活用を問われますから、これは当然のことですね。

つぎに、筆算について考えてみましょう。筆算の学習のポイントは位取りにありますが、それがほとんど思考不要のレベルでスッスッとできるようになっておく必要があります。もっと上の学年になった段階で、位取りでもたつくようでは勝負にならない学習場面が次々と出てくるからです。

あるおかあさんが、「うちの子は筆算が上手だから、九九なんてわざわざ覚える必要はありません」とおっしゃいました。この考えは正しいでしょうか。筆算は足し算や引き算だけではありません。やがて乗除算も登場してきます。そうなると九九の活用が必須となり、それが不十分なお子さんはたちまち躓いてしまいます。九九と筆算は、どちらも欠かせない基礎となる計算操作なのですね。

もう一つ押さえておきたい大事なことがあります。計算操作はできても、数の意味がわかっていなければ計算力が身についたとは言えません。計算式を自分で考えなければならない学習場面で躓いてしまうからです。たとえば、２～３行の簡単な文章題を通して考えてみましょう（３年生の課題です）。

とおるくんの弟は、６８５円もっています。弟のもっているお金は、とおるくんよりも２５２円少ないそうです。とおるくんは、いま何円もっていますか。

 

計算式が示された問題なら造作なくできても、このような問題が出されると、たちまち立ち往生するお子さんがいます。足し算か引き算かを自分で判断できないため、計算式が立てられないのです。これは計算の意味が理解できていないことに起因します。「足し算か、引き算か」のヒントがなければ答えられないお子さんは、真の計算力を備えているとは言えません。

だいぶ前のことですが、ある調査で、５分の４ｍ×３ｍという数式を用いた文章題をつくらせたところ、正解者は２割に満たなかったそうです（対象は５年生。数字は少し変えています）。誤答の例として、「５分の４ｍのつくえと、１ｍのいすを３つ買いました。ぜんぶで何ｍですか」などがあったとか。これは、掛け算と足し算の違いが理解できていないからでしょう。また、辺の掛算で長方形の面積が求まることも念頭にありません。これも計算の意味がわかっていないゆえの誤答です。

以上のように、計算力は意味の理解と操作の習熟とで支えられています。両者は互いに連動すべきものです。習熟的側面ばかりに目が向くと、ほんものの計算力は身につきません。高学年に進級した子どもたちが突き当たる算数の壁の代表的なものが小数と分数の計算ですが、これらも低学年期にほんものの計算力を身につけていれば問題なく乗り越えられます。今のうちに真の計算力を！

＜押さえておきたい！＞　できる、覚える、で満足していませんか？

１．計算ドリルは必須。だが、それだけでは不十分です。
計算力の習熟を図るうえでドリルへの取り組みは大変有効です。しかし、上述のように機械的に取り組むだけでは真の計算力は身につきません。お子さんには、実際場面を思い起こしながら　計算の式を立て、答えを導き出す学習も体験させてあげてください（この種の問題集もたくさんあります）。

２．図を描いて考える習慣を大切に！
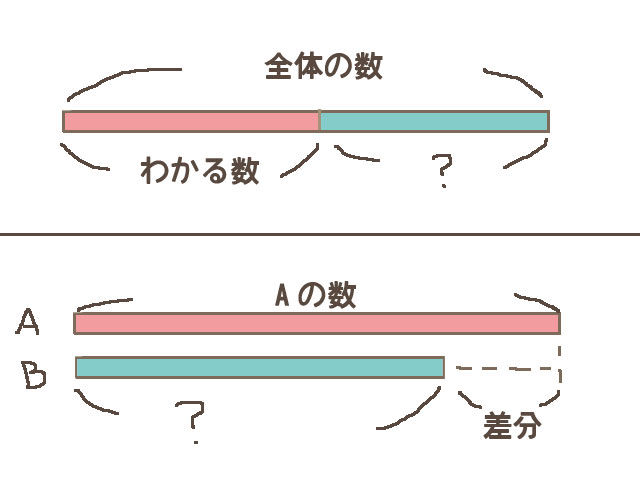 上述したお金の問題は、テープ図を描いて考えるとわかり易くなります。玉井式の「国語的算数教室」においても、テープ図を描いて考えるよう指導しています。できるお子さんは、図がなくても答えを容易に導き出せますが、そういうやりかたが通用するのは、問題の構造が単純だからです。やがて本格的な中学入試問題に取り組む段階が訪れたとき、図にして考える習慣は強力な武器となります。逆に、それをしなかったお子さんは行き詰まりがちです。図を描いて考える習慣を身につけておきましょう。